









 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
This page will first list a number of observations about the Voynich MS character statistics that may be found in the printed literature, and then concentrate on more quantitative analysis results.
(Note: Tiltman treats f as a variant form of k and p as a variant form of t. In the following, characters or sequences in parentheses represent such variant forms).
Currier's first observation has been noted independently by several people, and was taken up recently by Brian Cham, who developed the >>curve-line system out of it.
Oddly enough, there is no consolidated set of this most basic statistic, due to the use of different transliteration alphabets and different transliteration sources. Several examples may be found in different sources.
One example is found in D'Imperio (1978) (see note 4), Fig. 28 on p.106, from several sources but none covering the entire MS text.
I have produced some graphics of the single character frequency distribution of the entire MS, for four different transliterations. These may be found in the beginning of this page.
As a very short summary, the single character frequency distribution in the most important transliteration alphabets is largely similar to that of texts in normal European languages, thought the drop in frequency appears to be marginally steeper.
The concept of entropy has been explained in the introductory page and the reader should have read this introduction in order to properly appreciate the following.
The entropy of the Voynich MS text was first analysed in detail by the Yale professor William Ralph Bennett Jr. (6). He developed the concept in many easy steps and in more detail than in the above-mentioned introductory page. He first analysed texts in common European languages and then addressed the Voynich MS text, which he transliterated using his own transliteration alphabet (7). He writes (8):
[...] the statistical properties of the Voynich Manuscript are quite remarkable. The writing exhibits fantastically low values of the entropy per character over that found in any normal text written in any of the possible source languages (see Table 5). The values of h1 [i.e. first order entropy - RZ] are comparable to those encountered earlier in this chapter with tables of numbers. Yet the ratio h1/h2 is much more representative of European languages than of a table of numbers alone.
His computed values are as follows (9):
| Entropy order | Normal languages | Voynich MS |
|---|---|---|
| First | 3.91 - 4.14 | 3.66 |
| Second | 3.01 - 3.37 | 2.22 |
| Third | 2.12 - 2.62 | 1.86 |
He finally identified one language with a set of similarly low entropy values, namely Hawaiian, but he also pointed out that this is not likely to be significant.
More statistics related to entropy calculations may be found in an on-line paper by >>Dennis Stallings: understanding the second-order entropies of Voynich text. This basically confirms the results of Bennett. His descriptions will be useful for those who have no access to a copy of Bennett's book.
I have re-done the calculation for first- and second-order entropy for a larger number of languages, using the text of the Universal Declaration of Human Rights (10). This analysis will be described in more detail in a dedicated page, and for the moment I just show some of the results. In this analysis, the space character has not been interpreted as a character, but as a separator between words. The first plot below shows the (conditional) second-order entropy plotted against the first-order entropy, for a number of modern European languages, also including the results for the Voynich MS. The Voynich MS statistics are those computed by Bennett (left-most point) and those computed by Dennis Stallings for Herbal-A and Herbal-B using the Currier alphabet. The meaning of the legend is shown in a table below the figure. It is clear that none of the languages shows a similar behaviour to the Voynich MS text.
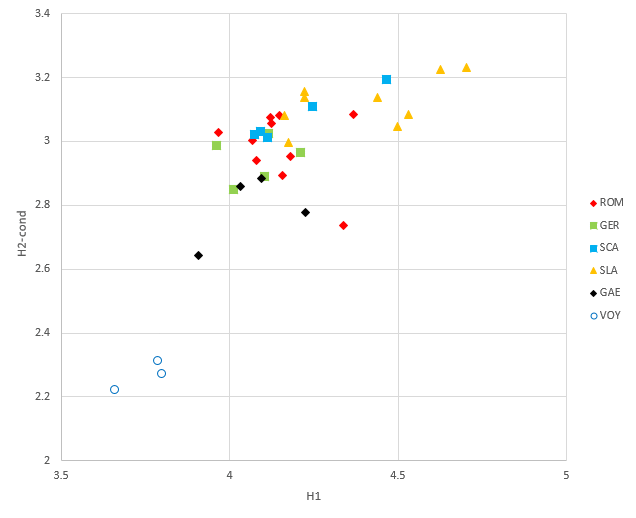
| Code | Meaning | Languages |
|---|---|---|
| ROM | Romance languages | Latin, French, Spanish, Italian, Portuguese, Catalan, Galician, Occitan (Auvergnan), Corsican, Friuli, Maltese |
| GER | Germanic languages | English, German, Dutch, Frisian, Afrikaans |
| SCA | Scandinavian languages | Swedish, Norwegian (Modern and Bogmål), Danish, Icelandic |
| SLA | Slavic languages | Russian, Polish, Czech, Slovak, Croatian, Bulgarian, Macedonian, Belorus, Georgian |
| GAE | Gaelic languages | Scottish Gaelic, Irish Gaelic, Breton, Manx |
The calculations have been repeated for a number of other languages from around the world. These are listed in the following table:
| Code | Meaning | Languages |
|---|---|---|
| EUO | European, other | Albanian, Basque, Finnish, Hungarian |
| AFR | African | Ethiopian (Amharic), Swahili, Hausa, Edo, Somali, Bari |
| IEU | Indo-European | Greek, Estonian, Latvian, Lithuanian, Farsi, Hindi, Nepali, Urdu |
| DRA | Dravidian | Malayalam, Kannada |
| ASI | Asian | Turkish, Armenian, Turkmen, Kurdish, Hebrew, Arabic, Azerbaidjani, Bengali, Minjiang (a Chinese dialect, spoken vs. written), Tibetan, Mongolian, Japanese, Korean, Thai, Laotian, Burmese, Cambodian, Vietnamese, Indonesian, Tagalog, Cebuano, Hawaiian |
The result is shown in the following plot, where the points for the "European" languages have been repeated in grey.
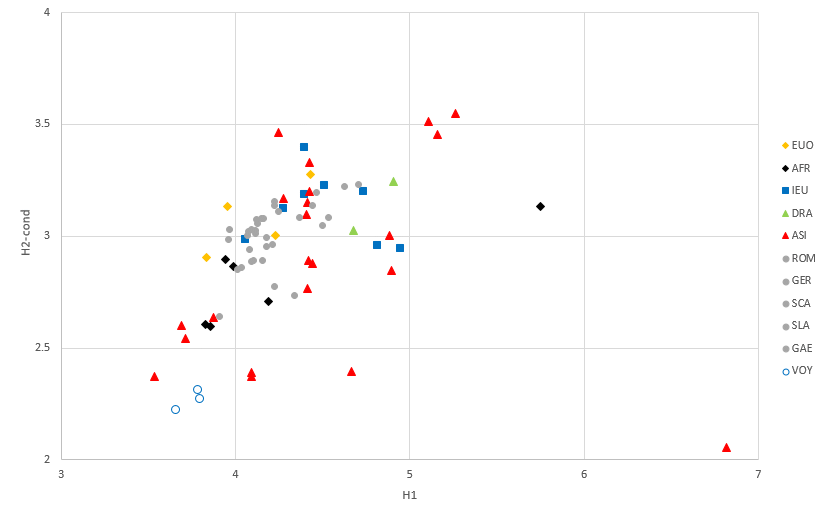
Here we see a number of points among the group of Asian languages that lie in the relative vicinity of the Voynich MS text. The lowest and leftmost point is Tagalog (Philippinian). The two points to the right of this are the spoken and written version of Minjiang. These text have been written in the Latin alphabet without indication of tones. Hawaiian, the language named by Bennett, is the lowest point directly above those for the Voynich MS.
A more recent study by Luke Lindemann and Claire Bowern of Yale University (11) covers some of the same ground, and analyses even more different languages, including historial corpora. It comes to the same conclusion and summarises:
The character set size and frequency of characters is conventional, but the characters are combined in an extremely predictable way, as indicated by an unusual conditional character entropy that is distinctly lower than any of the 316 comparison texts. This discrepancy is not attributable to the transcription system used to encode Voynich, although decisions about the compositionality of glyph sequences can have a significant effect on entropy. Nor is it the result of conventional scholarly abbreviations of the historical period or the absence of written vowels. Rather, it is largely the result of common characters which are heavily restricted to certain positions within the word. Voynichese most closely resembles tonal languages written in the Latin script and languages with relatively limited syllabic inventories.
An alternative method to compute entropy is the so-called 'commas' method, which has been used by Jim Reeds and later by Gabriel Landini. This will be included here at some future time.
Jorge Stolfi has set up a tool to visualise the number of bits of entropy per character in the following location: >>Jorge Stolfi: where are the bits?
Furthermore, I have addressed the question how it is possible that the character and bigram entropy of the Voynich MS text is so much lower than that of, say, Latin, while the word entropy (about which something will be said here) is similar. This is addressed at this page: From bigram entropy to word entropy. I realise that this page is rather hard to understand in its present form, and I will re-do it. The short summary is that, counting from the start of each word, the entropy per character in the Voynich MS starts off lower for the first two characters, but is higher for the remainder of the characters, when compared to normal languages.
While the entropy values are single values derived from a frequency distribution, more can be learned by looking at the detail of these distributions, for which see here. This discussion exemplifies even better how much different the Voynich MS text is from 'regular languages'.
There is a critically important conclusion to be drawn from the first- and second-order entropy values reported by various authors. As already mentioned in the analysis section introduction, the entropy values do not change when one consistently replaces characters by others, i.e. in a simple substitution cipher. This tells us something about the possible plain text of the Voynich MS.
In general, and quite briefly, any attempt to translate the Voynich MS into something meaningful in Greek, Latin, English, etc. using a simple substitution must fail. As this is the first thing most people will try, we can begin to understand how the MS has resisted all translation attempts.
However, there is much more to this, as we shall see in the following (12).
An algorithm for detection of vowels and consonants was designed by B.V. Sukhotin, and Jacques Guy has experimented with this in the 1990's. He published a first English summary of the algorithm in Cryptologia (see note 5). Results indicated that the characters that look like vowels (a, o, y) also appeared statistically like vowels, though the confidence of the result was not very high. There is also a more recent >>internet blog entry related to running Sukhotin's algorithm on individual pages of the MS.
Significant further work on vowel/consonant detection has been done using Hidden Markov Modelling, which is summarised in the next section.
This technique has been introduced briefly on a previous page. There are not many publications that discuss its application to the Voynich MS. Following is a summary.
Jeffrey Krischer
Techniques similar to HMM processing were initially classified, and publications of its application have been
restricted. D'Imperio mentions
(see note 4)
a first application of this in a paper by Jeffrey Krischer. He also published an unclassified summary
(13),
which does not give any details about the method and the results.
Mary D'Imperio
Mary D'Imperio made her own analysis, which was published in an undated paper that was also classified, but
has been de-classified and released a few years ago
(14).
During the de-classification, some parts of the text have been blanked out, but sufficient details have remained
to be able to conclude that the method she used, which was known by the name PTAH, was indeed an implementation
of a Hidden Markov model. In the paper she used a five-state model and applied it both to an English text, and
a transliteration of the Voynich MS text which consisted of 3113 characters from Currier's transliteration
of the "Biological B" section.
Using relatively clear hand-drawn diagrams, she demonstrates that English and "Voynichese" behave completely differently. In English, the five states can follow each other back and forth, while in Voynichese, the five states tend to form a cycle, which is followed in a single direction.
Interstingly, she has also managed to apply the method not only to single letters, but to word fragments and to words. This requires further study before I can explain it here.
Her conclusion of this work is stated quite clearly (even though she expresses that she does not wish to sound too positive):
Jim Reeds
Jim Reeds may have made similar analyses, but these have not been published as far as I know. I have some
information about this from personal communication with him. He summarised that, while for known languages
the HMM tends to separate vowels and consonants, for the Voynich MS text the analysis brings out a circular
pattern of characters. This is the same as what D'Imperio found and published, as described above, and it
may be that this is simply what he described to me.
Reddy and Knight
One of the analyses reported in Reddy and Knight (2011)
(15)
is the application of a two-state bigram HMM to the characters in the Voynich MS words. They report that
normally, in alphabetic languages like English, the clusters correspond almost perfectly to vowels and
consonants. They find, however, that with the Voynich MS the last character of every word is generated by one
of the HMM states, and all other characters by another, i.e. as if the vowels are at the end of each word.
They speculate further on this point in their paper. I have not been able to reproduce this feature myself.
Later work
A more recent paper by Acedo
(16)
describes a single application of a two-state HMM to the Takehashi transliteration of the MS, where he
tentatively concludes that this successfully shows a separation into vowels and consonants.
I have started a more comprehensive analysis myself, which is still under work, and which is summarised in this page. At the present stage, this seems to indicate that the separation into vowel- and consonant states is not nearly as clear as for known plain texts.
Following observations are paraphrased from Currier's papers (see note 3).
The obsernation of Currier that the line appears to be a functional unit was further analysed in 2012 by Elmar Vogt, for which >>see here. One of the most obvious features he shows is that, when using the Eva alphabet, the first word tends to be on average 1 character longer than the second and following words.
Julian Bunn highlighted the positions of the gallows characters on each folio of the MS in >>a page at his blog, in colour coded graphics. They show a peculiar vertical pattern, which may be related to the observations of Andreas Schinner in his 2007 cryptologia paper (19), which is discussed in a later page.
The following page by Sean V. Palmer gives a very visual representation of the feature that many characters have very preferential positions inside the words of the MS: >>Voynich MS glyph position stacks.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |